Yeast population growth

I started educating beer judges two months ago and the upcoming topic will be 'fermentation'. This peaked my curiosity a little. I do have two text which cover this. This is Heinrich Lüers "Wissenschaftliche Grundlagen von Mälzerei und Brauerei" and White and Zainasheff "Yeast". Lüers is more of a basic science text, written in 1950, while White is specifically aimed at the ambitious homebrewer and maybe the microbrewer.

Let's review Lüers most important ideas.

Yeast population growth

Lüers give for the population growth:

$$ N_f = N_0 e^{kt} $$

With \(N_0\) the initial mass, \(N_f\)the end mas and \(k\) the growth constant.

This, he states, is reformulated for \(k\)

$$ k= (\log N_f - \log N_0) / 0.4343 *t $$

More precisely^[1]

$$k= (\ln N_f - \ln N_0) / t$$

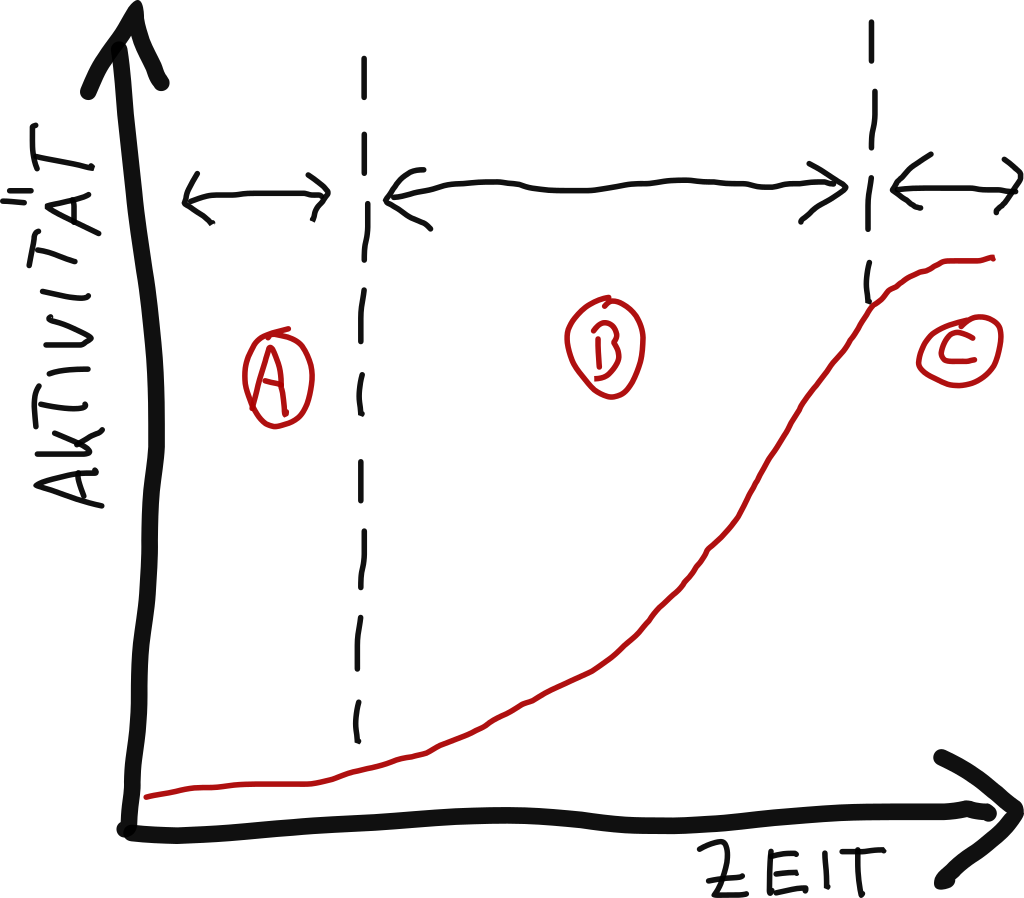
He states that this rule will hold true for the initial growth phase, but that growth will diminish once nutrients are metabolized by the yeast.

He gives as the generation time

$$g=t*\log 2/(\log b - \log a)$$

With \(a\) and \(b\) as the cell count at the beginning and end of the experiment respectively^[2].

Lüers give the generation time for a yeast that was grown according to Hägglund (mineral salt added to solution) as 8 hours 17 minutes. The same yeast has a generation time of 4 hours and 12 minutes, when a small amount of autolyzed yeast is added to the solution. He gives another example of wort with fine trub having a generation time of 5.5 hours, while those without fine trub has a generation time of 3 hours.

As a rule of thumb, Lüers give a generation time between 5 and 9 hours in beer wort.

The role of temperature

Lüers cites Bertalanffry in attributing two differences in fermentation: with increasing temperature the fermentation process increases, but the individual cell size at the end will decrease. He attributes this to the fact that the mitosis rate grows faster than the cells ability to assimilate nutrients, hence resulting in more, but smaller cells.

For a lager yeast, he lists the following generation times:

• 4°C: 20 hours
• 13°C: 10.5 hours
• 23°C: 6.5 hours
• 28°C: 5.8 hours
• 38°C: no growth

He notes that the maximum growth will be reached between 27.5°C and 30°C.

As the pasteurization temperature for yeast, he lists 58-60°C for a yeast culture with the name "Saaz". In the same vein he relates the fact that yeast can be deep frozen for multiple months, without killing it. He states that the main problem of freezing is the speed at which the yeast is cooled and the temperature it's stored at. It should be frozen quickly and stored at or below -20°C.

Lastly sporulation optima lie at different temperatures^[3].

Other factors

We still need to investigate wort concentration, alcohol concentration as well as oxygen content of wort.

White and Zainasheff relate the fact, that most of the aromatic compounds produced by the yeast, will already be formed during the exponential growth phase.

We will observe White and Zainasheff in a later post and hopefully get to some more details about fermentation.

Footnotes